As I mentioned in an earlier post about tiling patterns, I really like truchet tilings. Each border of the tiles that traditionally have patterns that connect the midpoints of adjacent sides. I explored this concept a long time ago, but instead of using a traditional square grid, I used a hexagonal one instead.
Each hexagon has every side connected to another side, and by repeating these connections, you end up with some emergent structures of how the paths travel over time. I like calling them noodles, so that’s what I’ll do here from now on.
My original implementation was… a bit of disaster from the code perspective. I left it for a while, and when I went back to revisit it to color each of these noodles individually, I found myself confused by my own work and gave up. Later on, I still felt the urge to do improve upon my initial version and recreating it from the ground up seemed like the fastest option.
New Implementation
Paths Generation
I built upon my initial idea of defining a grid of flat-top hexagons, and added some definitions to keep things clear. Each side of the hexagon is assigned an index integer, as well as a list of integer pairs to define which sides of the hexagon are connected. Each hexagon could contain zero to three sets of connections, with their order denoting the order in which they would be drawn to the screen.
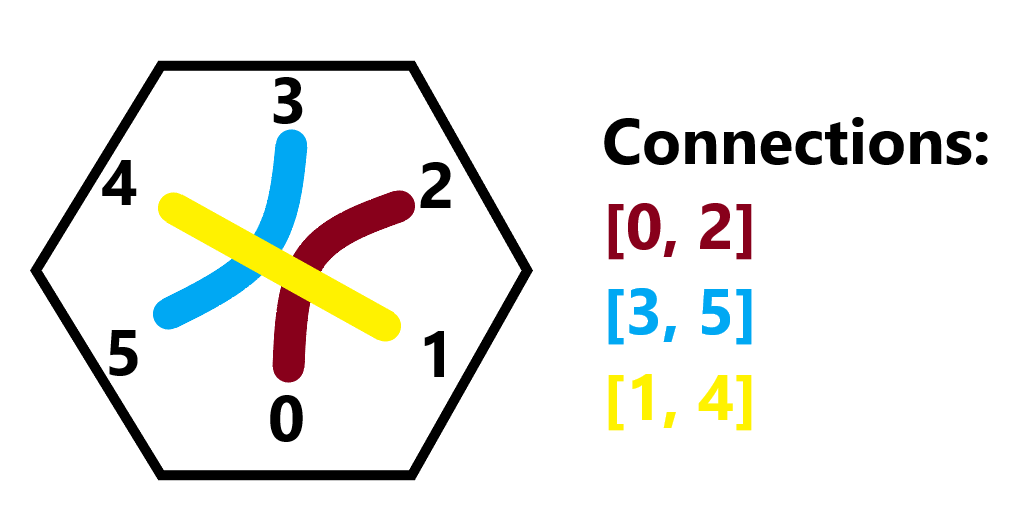
Once we generate connections for each of the hexagons, we iterate over all the hexagons and over all the connections for each hexagon. We start at the first connection, and if it has not been visited, recursively follow the path from one hexagon to the next, using the side indices we defined earlier to choose the next hexagon, until we reach an end, a visited path, or the starting point. As we traverse them, we mark each of the connections as visited, so that when we reach that connection later on, we will not pursue it. One note is that, since we don’t know whether or not we are starting at an endpoint, we traverse the path in two different directions, and just swap the connection orders for one of the directions before combining.
The result for following a single path in how it maps across hexagons can be shown below:
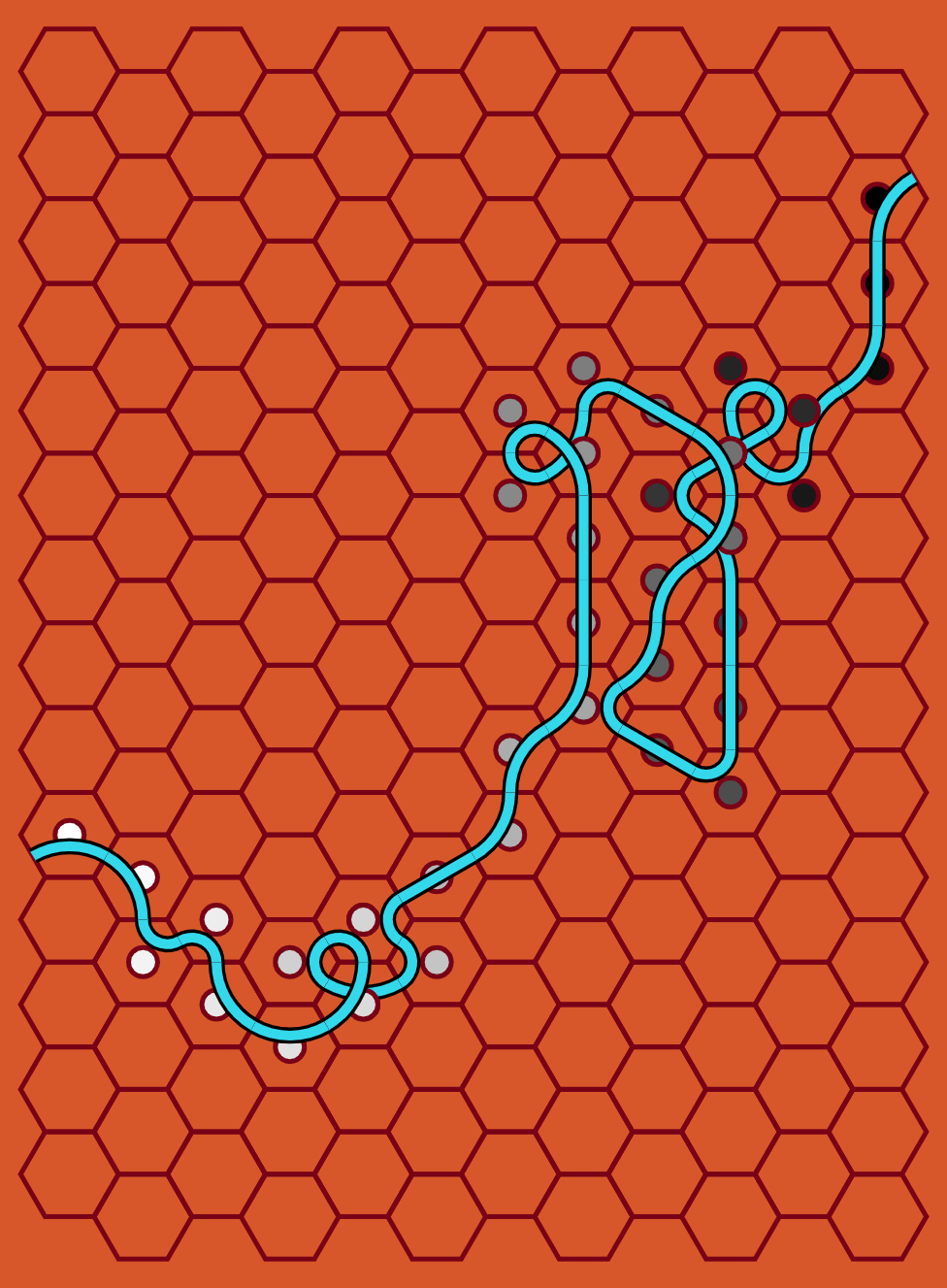
We do this for all hexagons and all connections, collecting them into path objects with their hexagon locations and x/y coordinates. Once this is finished, we have all our paths and just need to cap them with semicircles of the correct end colors. Here is a final render of all paths being drawn without caps, overlaid with the hexagon grid that underlies them all.

At this point, we have all we need and just need to assign the colors and work on generating interesting patterns.
Style Generation
While there were dozens of ideas I could have explored, I get overwhelmed with too many options so I limited myself to the following areas to delve deeper into and came up with the following final list of constrainted parameters that I chose to work within.
- Colors
- Overall palette
- What do we want to use for the background and noodle colors?
- Even if a palette is good, does it have enough contrast to distinguish between foreground/background?
- Does the palette have muddy colors if we have a gradient or do the in between colors look good as well?
- Noodle style
- Color it directly or add an outline surrounding it
- If we have an outline, do we keep a static one across all noodles or pick a different outline color for each?
- Color the noodle with a single color or make a color changing graadient
- If we have a gradient, do we rotate through the palette in order or assign sequential colors randomly?
- Color it directly or add an outline surrounding it
- Overall palette
- Path shapes
- Connection patterns
- Fully random for each hexagon
- Do we keep three sets of connections for each one or do we have a lower amount?
- Stripes along horizontal, vertical and diagonals
- Chunks of MxN hexagon groups that are repeated along horizontal, vertical and diagonals with or without offsets
- Fully random for each hexagon
- Border
- Do we feed connections back to the middle or just truncate?
- Curve polygon fidelity
- Closer to fully round
- Low poly
- Connection patterns
Ultimately, I think my favorites were gradient noodles without outlines that either had random connections or repeating chunk patterns.


